Implementing LLaMA3 in 100 Lines of Pure Jax
In this post, we'll implement llama3 from scratch using pure jax in just 100 lines of code. Why jax? Because I think it has good aesthetics. Also jax looks like a NumPy wrapper but it has some cool features like xla; a linear algebra accelerator, jit, vmap, pmap etc., which makes your training go brr brr.
Jax is one of the first libraries which strongly focuses on the soul of pure functional programming which makes it more cool.
Note
- This post assumes familiarity with Python and basic understanding of transformer architectures.
- This implementation is for educational purposes, which means it is not for any production stuff but it covers all components of the model.
- If you don't wanna read this amazing blog post then you can check out all the code at this repository.
LLaMA3
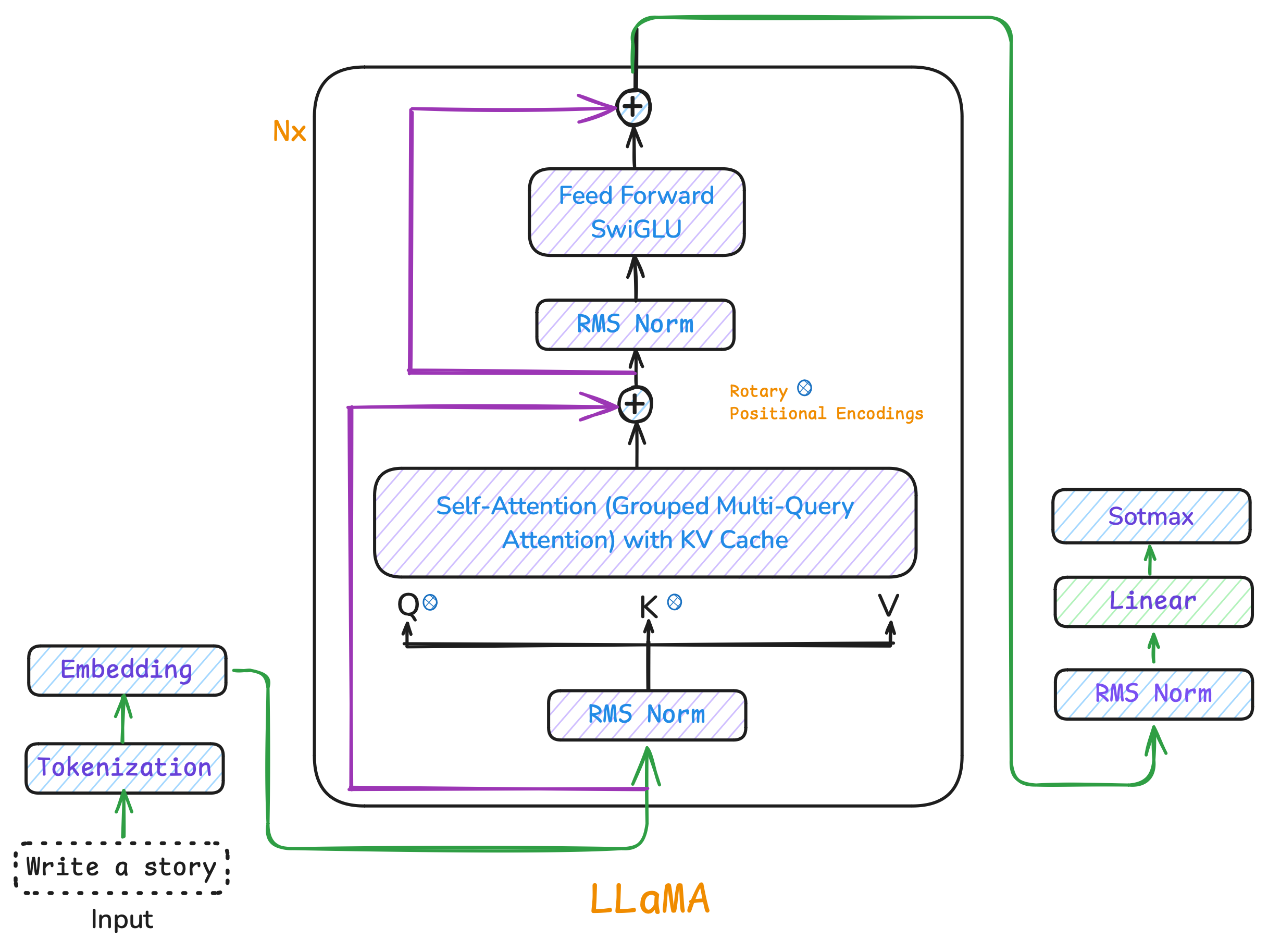
Figure 1: LLaMA3 Architecture Overview
At its core, LLaMA 3 is a decoder only transformer language model that generates text one token at a time, building on previous tokens to predict what comes next ; like completing a sentence word by word.
So lets fucking go !! we're doing it, get your diet coke !! First, we will begin with setting up device and configuring the model.
# Configure JAX to use GPU and prevent memory preallocation
os.environ['JAX_PLATFORM_NAME'] = 'gpu'
os.environ['XLA_PYTHON_CLIENT_PREALLOCATE'] = 'false'
print("JAX devices:", jax.devices())So these are the hyperparameter we need to train approximately 2 million parameters model.
# Define model hyperparameters
args = ModelArgs(
vocab_size=enc.n_vocab, # Size of vocabulary
dim=256, # Embedding dimension
n_layers=6, # Number of transformer layers
n_heads=8, # Number of attention heads
n_kv_heads=4, # Number of key-value heads for GQA
max_seq_len=512, # Maximum sequence length
norm_eps=1e-5 # Normalization epsilon
)Model Weights Initialization
In pure JAX, we don't use classes like in PyTorch. We use only pure functions why ? cause it makes our code more predictable and easier to parallelize. A pure function always returns the same output for the same input and doesn't cause any side effects. For example, if you call F(x), you'll always get the same y.
Since we aren't using a framework like PyTorch's nn.Module to automatically track parameters, we must initialize and update our weights manually.
Handling randomness is also different. Instead of relying on a single global seed as in NumPy or PyTorch, in jax we need to manage randomness with explicit pseudo-random number generator (PRNG) keys. Each random operation gets its own unique key, which is derived by splitting a parent key. This will help in reproducibility and parallelism.
# Generate and split random keys for reproducibility
key = jax.random.PRNGKey(42)
# Create a new subkey for random operations
key, subkey = jax.random.split(key)
# Initialize random weights using the subkey
weights = jax.random.normal(subkey, (784, 512))Now lets start with our Model Weights Initialization, first we create the random values for our parameters with normal distribution.
def init_weight(key, shape, scale=None):
# Calculate default scale if none provided
scale = 1.0 / math.sqrt(shape[0]) if scale is None else scale
# Return scaled normal distribution
return jax.random.normal(key, shape) * scaleTokenization
Tokenization means dividing the text into words and subwords (tokens). We will be using Byte Pair Encoding (BPE) for training our model (BPE was used in training Llama 3). I will not build bpe from scratch we will use tiktoken library by openai for bpe.
import jax.numpy as jnp
import tiktoken
# Load GPT-2 BPE encoding
enc = tiktoken.get_encoding("gpt2")
# reading a line from
with open('../shakespeare.txt', 'r') as f:
text = f.readlines()[0] # Take the first line
# Encode the text into token IDs
tokens = enc.encode(text)
data = jnp.array(tokens, dtype=jnp.int32) # Store as JAX array
# Decode back to text
decoded_text = enc.decode(tokens)
print("original Text:", text.strip())
print("encoded Tokens:", tokens)
print("decoded Text:", decoded_text)Embeddings
We cannot provide tokens directly to a model because tokens are discrete, while neural networks operate on continuous numerical data this is important for performing mathematical operations. Therefore, we use an embedding layer to convert the discrete tokens into a continuous vector space. These embeddings also help encode the semantic and syntactic relationships between tokens.
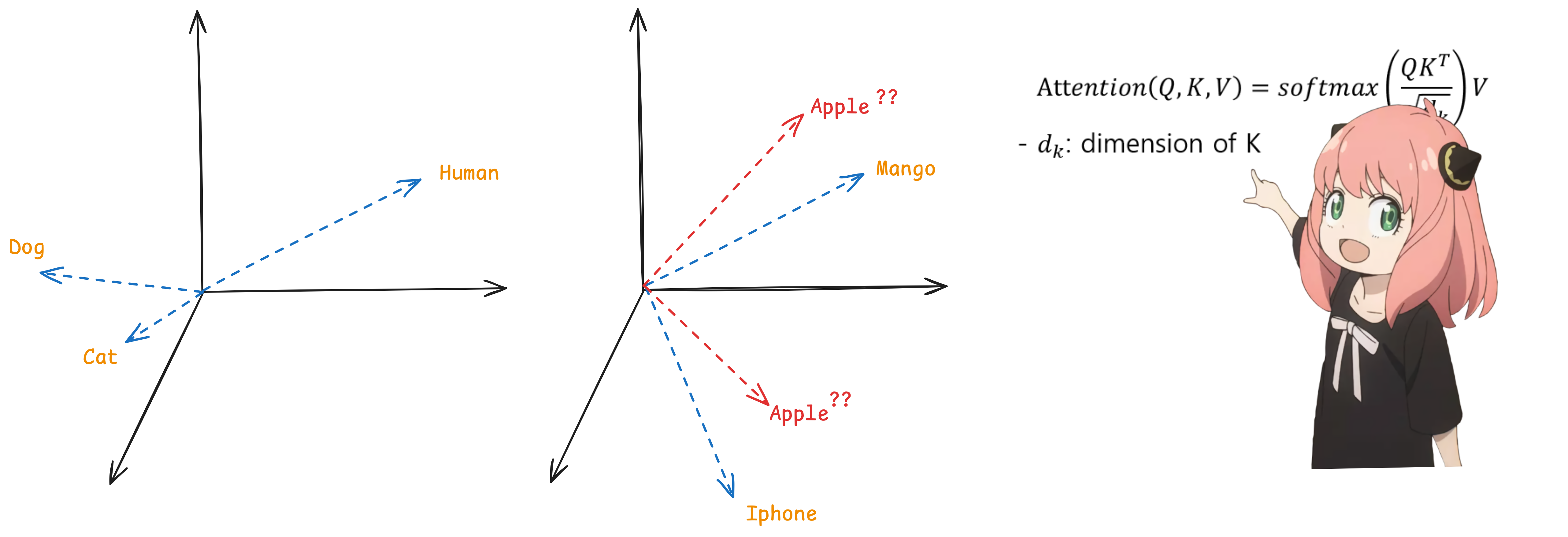
Figure 2: Embeddings
There are two types of embeddings: static and dynamic. We use dynamic embeddings to train LLMs. Why? Because static embeddings work well for finding similarities between words and representing them in a similar vector space.
However, they suffer from semantic ambiguity. This is where Self-Attention comes in, it refines these embeddings to incorporate context. So, we start with random embeddings and update them according to the context.
# Converting the input tokens into embeddings
h = params["token_embedding"][inputs]
# token_embedding is a matrix of shape (vocab_size, dim).
# inputs are token IDs (integers).
# token_embedding is a matrix of shape (vocab_size, dim).Root Mean Square Layer Normalization
RMS normalization is an important layer in llama3 models. It helps keep the training stable by making sure that the numbers in the network don't become too high or too low. This balance is very important, especially in deep networks.

Figure 3: RMS_NORM
# RMS Norm function for stabilizing training
def rms_norm(x, weight, eps=1e-5):
# Calculate variance across last dimension
variance = jnp.mean(jnp.square(x), axis=-1, keepdims=True)
# Normalize and scale
return x * weight * jnp.reciprocal(jnp.sqrt(variance + eps))Rotary Positional Encoding
Transformers don't naturally know the order of tokens, so we need to add some position info. In llama3 to solve this we have ROPE. It does this by "rotating" the query and key vectors based on their position.
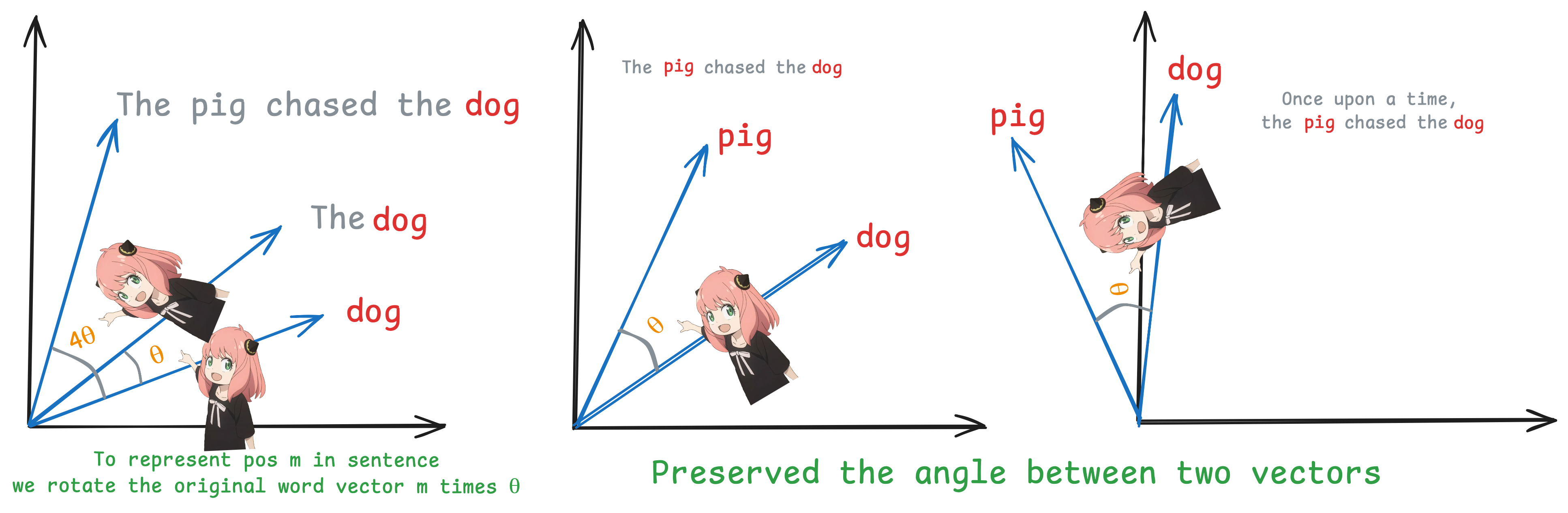
Figure 3: Rotary Positional Embeddings
How It Works:
Precompute Rotation Factors: First we create a table of rotation factors using a range of frequencies. This means each token gets its own unique rotation angle.
# Compute rotary position embeddings
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
# Generate frequency bands
freqs = 1.0 / (theta ** (jnp.arange(0, dim // 2, dtype=jnp.float32) / dim))
# Generate position indices
t = jnp.arange(end, dtype=jnp.float32)
# Compute outer product
freqs = jnp.outer(t, freqs)
# Convert to complex exponential
return jnp.complex64(jnp.exp(1j * freqs))Apply the Rotation:
- Pair Up Features: we reshape the vectors so that every two numbers form a pair; imagine them as the real and imaginary parts of a complex number.
- Rotate: We multiply these complex numbers by our precomputed rotation factors. This rotates each pair in the complex plane.
- Convert Back: Finally, we split the rotated complex numbers back into their real and imaginary parts to restore the original shape.
Math Behind It:
For each pair (x2i,x2i+1)(x2i,x2i+1), the rotation is given by:
(x′2ix′2i+1)=(cos(θi)−sin(θi)sin(θi)cos(θi))(x2ix2i+1)
where θi is the rotation angle for that token.
Group-Query Attention
Now it's time for attention. Grouped Query Attention (GQA) is an optimized version of Multi-Head Attention that improves efficiency by sharing key and value representations among multiple query heads. This reduces computational overhead and memory usage, enabling faster inference and better scaling for transformer models.
Scaled Dot-Product Attention:
A=softmax(QKT√dh)V
# Attention mechanism with grouped-query attention
def attention(params, x, mask, freqs_cis, n_heads, n_kv_heads, cache=None, position=0):
# Get input dimensions
B, T, C = x.shape
head_dim = C // n_heads
# Project inputs to queries, keys, and values
q = jnp.dot(x, params['wq']).reshape(B, T, n_heads, head_dim)
k = jnp.dot(x, params['wk']).reshape(B, T, n_kv_heads, head_dim)
v = jnp.dot(x, params['wv']).reshape(B, T, n_kv_heads, head_dim)
# Apply rotary embeddings
q, k = apply_rotary_emb(q, k, freqs_cis[position:position + T])
# Handle cache for inference
if cache is not None:
k = jnp.concatenate([cache[0], k], axis=-1)
v = jnp.concatenate([cache[1], v], axis=-1)
new_cache = (k, v)
# Repeat k/v heads for grouped-query attention
k = repeat_kv(k, n_heads // n_kv_heads)
v = repeat_kv(v, n_heads // n_kv_heads)
# Compute attention scores and apply attention
q, k, v = map(lambda x: x.transpose(0, 2, 1, 3), (q, k, v))
scores = jnp.matmul(q, k.transpose(0, 1, 3, 2)) / math.sqrt(head_dim)
# Apply attention mask if provided
if mask is not None:
scores = scores + mask[:, :, :T, :T]
# Compute attention weights and final output
scores = jax.nn.softmax(scores, axis=-1)
output = jnp.matmul(scores, v)
output = output.transpose(0, 2, 1, 3).reshape(B, T, -1)
return jnp.dot(output, params['wo']), new_cacheKV Cache
KV cache stores the Key (K) and Value (V) tensors from previous decoding steps. So they don't need to be recomputed every time a new token is generated.
And it don't need to go through all previous steps, reducing computation from O(n²) to O(n) per step and making generation much faster.
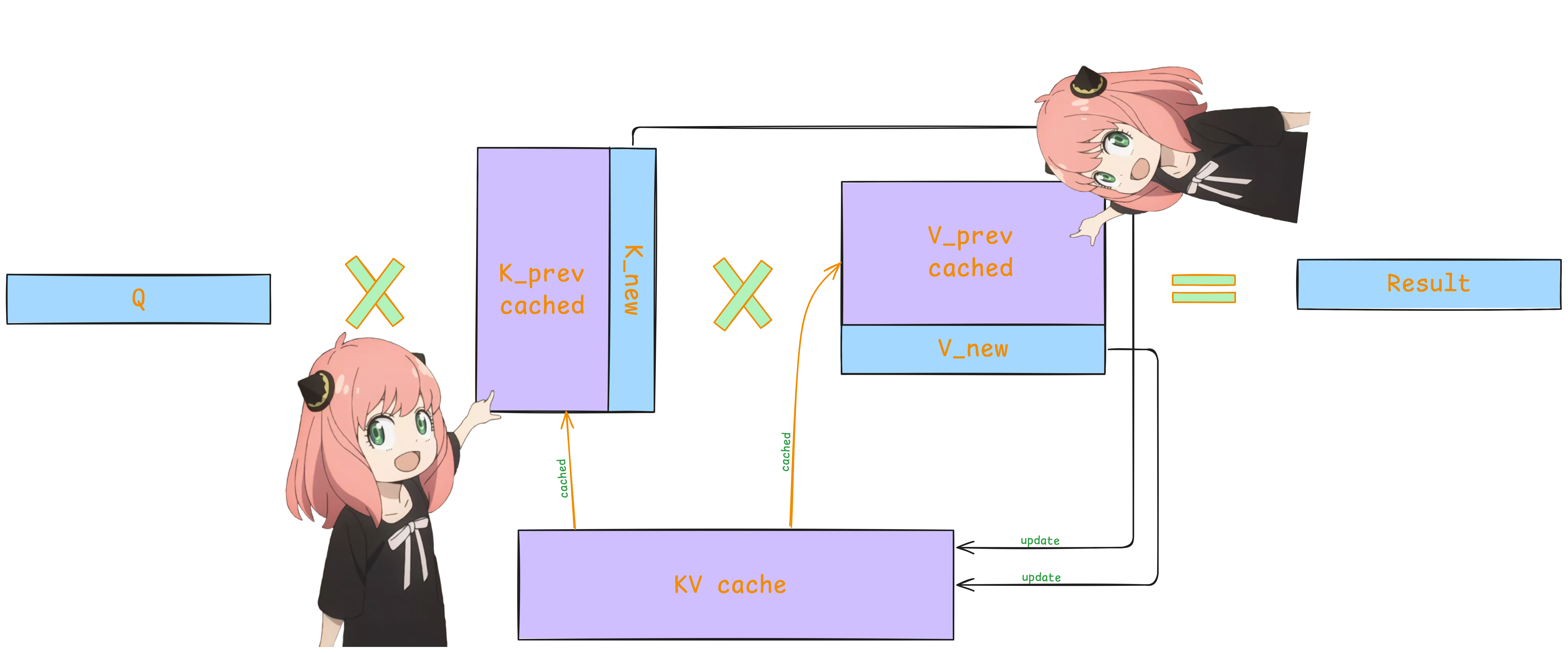
Figure 4: KV Cache
Feed-forward
This is simple feed-forward network with SiLU activation function.
def feed_forward(params, x):
w3_ = jnp.dot(x, params['w3'])
# SwiGLU(a,b)=SiLU(a)⊙b
activated = jax.nn.silu(w3_)
w1_ = jnp.dot(x, params['w1'])
combined = activated * w1_
# Final output projection with w2
output = jnp.dot(combined, params['w2'])
return outputTransformer-block
This is where all the important components come together in the transformer block. We unpack the pre-initialized weights and distribute them to their respective layers. The transformer blocks include attention, normalization, feed-forward processing layers and residual connections.
# Transformer block implementation
def transformer_block(params, x, mask, freqs_cis, n_heads, n_kv_heads, cache=None, position=0):
# Apply attention with normalization and residual connection
attn_output, new_cache = attention(
params['attention'],
rms_norm(x, params['attention_norm']),
mask,
freqs_cis,
n_heads,
n_kv_heads,
cache,
position
)
# First residual connection
h = x + attn_output
# Apply feed-forward network with normalization and residual
ffn_output = feed_forward(params['ffn'], rms_norm(h, params['ffn_norm']))
# Second residual connection
out = h + ffn_output
return out, new_cacheForward-Pass
The forward pass takes your data through the entire model from converting input tokens into embeddings, through a series of transformer blocks, and finally to the output layer. In other words, it connects all the layers (embedding, transformers, and output) to produce the final predictions.
# Forward pass through the entire model
def model_forward(params, inputs, config, cache=None, position=0):
# Get batch dimensions
B, T = inputs.shape
# Convert input tokens to embeddings
h = params['token_embedding'][inputs]
# Compute freqs_cis for this forward pass
freqs_cis = precompute_freqs_cis(config.dim // config.n_heads, config.max_seq_len)
# Create causal mask
mask = jnp.tril(jnp.ones((config.max_seq_len, config.max_seq_len)))
mask = jnp.where(mask == 0, -1e9, 0.0)
mask = mask.astype(h.dtype)
mask = mask[None, None, :, :]
# Process through transformer blocks
new_caches = []
for i, block in enumerate(params['blocks']):
layer_cache = cache[i] if cache is not None else None
h, layer_cache = transformer_block(
block, h, mask, freqs_cis,
config.n_heads, config.n_kv_heads,
layer_cache, position, training=False)
new_caches.append(layer_cache)
# Final normalization and output projection
h = rms_norm(h, params['norm_f'])
logits = jnp.dot(h, params['output'])
return logits, new_cachesDataset
Now the model part is complete so its time to train our model on shakespeare dataset. First we will read our data from .txt file then we will encode our data with bpe and then convert it into jax array.
# Initialize tokenizer and load data
enc = tiktoken.get_encoding("gpt2")
# Read text file
with open('shakespeare.txt', 'r') as f:
text = f.read()
# Convert text to token IDs
tokens = enc.encode(text)
# Convert to JAX array
data = jnp.array(tokens)Get Batches
The get_batch function creates training batches from our Shakespeare dataset. We need to feed our model with chunks of data. For each batch, we randomly select starting positions in the text, this way the model sees a variety of contexts.
Now, here's where JAX's cool vmap feature comes into play. Instead of writing a loop to extract each chunk, we use vmap to automate.
How does it work?
vmap is like a vectorized loop; it takes a function that processes a single index (using lax.dynamic_slice to get a sequence of tokens) and applies it to every element in our array of indices. This means our input sequences (x) and corresponding target sequences (y, which are shifted by one token for next-word prediction) are created in one go.
def get_batch(key, data, batch_size, seq_len):
# Generate random starting indices
ix = random.randint(key, (batch_size,), 0, len(data) - seq_len)
# Vectorized operation to get input and target sequences
x = vmap(lambda i: lax.dynamic_slice(data, (i,), (seq_len,)))(ix)
y = vmap(lambda i: lax.dynamic_slice(data, (i + 1,), (seq_len,)))(ix)
return x, yLoss Function
This function computes the cross-entropy loss for a batch during training. It first performs a forward pass using the model to generate logits for the input data. Then, it reshapes both the logits and targets to merge the batch and sequence dimensions. After applying the log softmax to the logits, it extracts the log probabilities corresponding to the correct target tokens and computes their negative mean as the final loss value.
The cross-entropy loss is defined as:
L=−1NN∑i=1logP(yi)
Where P(yi) is the probability of the correct class, calculated using the softmax function:
P(yi)=ezi∑jezj
# Compute cross-entropy loss
def compute_loss(params, batch):
# Split batch into inputs and targets
inputs, targets = batch
# Forward pass to get logits
logits, = model_forward(params, inputs, config)
# Reshape for loss computation
logits = logits.reshape(-1, config.vocab_size)
targets = targets.reshape(-1)
# Calculate negative log likelihood
loss = -jnp.mean(jnp.take_along_axis(jax.nn.log_softmax(logits),
targets[:, None], axis=1))
return lossUpdate function
Now we need to write a function to update our weights. For simplicity, we're using Stochastic Gradient Descent (SGD) here, though you can also use Adam or AdamW for faster convergence.
In the code, you'll notice the @jax.jit decorator. This is one of the features that sets jax apart. JIT (Just-In-Time) compilation speeds up execution by converting your Python code into optimized machine code.
@jax.jit
def update_step(params, batch):
# Compute both loss and gradients in a single pass using value_and_grad
# This is more efficient than computing them separately
loss, grads = jax.value_and_grad(compute_loss)(params, batch)
# Update parameters using gradient descent
# jax.tree.map applies the update rule to each parameter in the model
# The lambda function implements: p_new = p_old - learning_rate * gradient
params = jax.tree.map(
lambda p, g: p - config.learning_rate * g,
params,
grads
)
# Return updated parameters and the loss value for monitoring training
return params, lossTraining-Loop
Finally, its time to train our 2 million parameter model on shakespeare dataset. We first prepare batches using the get_batch which splits our data into batches so we can train faster with our limited compute.
for epoch in range(num_epochs):
epoch_loss = 0.0
for step in range(steps_per_epoch):
# Generate new random keys for reproducibility
key, batch_key = random.split(key)
# Sample random batch of sequences
batch = get_batch(batch_key, data, config.batch_size, config.max_seq_len)
# Forward pass, compute loss and update parameters
params_state, loss = update_step(params_state, batch)
# loss for epoch average
epoch_loss += loss
if step % 100 == 0:
print(f"epoch {epoch + 1}, step {step}/{steps_per_epoch}: loss = {loss:.4f}")
avg_epoch_loss = epoch_loss / steps_per_epoch
epoch_losses.append(avg_epoch_loss)
print(f"\nepoch {epoch + 1} | average loss: {avg_epoch_loss:.4f}")Thank you for reading!
You can support me: